 CS227:Assignment
1
CS227:Assignment
1
MATLAB Basics, and some Plotting Exercises
Assigned: Tuesday, September 6
Due: Tuesday, September 13
Due: Tuesday, September 13
Relevant reading: Lecture
Notes 1. From Hunt, Chapter 2 (don't bother for now with the
sections about symbolic computation
and matrices) and the first six pages of Chapter 5. From Moler,
Sections 1.1 and 1.7.
From Driscoll: Chapter 1, Sections 2.1-2.4, and Section 5.1.
You will need to turn in (among other things) a file contaning the MATLAB commands that you type in order to solve the problems below, so once you complete a problem, you should select, copy and save a transcript of your session, or, better yet, create M-files. (See "What to Hand In" below for more detail.)
You will need to turn in (among other things) a file contaning the MATLAB commands that you type in order to solve the problems below, so once you complete a problem, you should select, copy and save a transcript of your session, or, better yet, create M-files. (See "What to Hand In" below for more detail.)
1. Harmonic series and summation order
The harmonic series
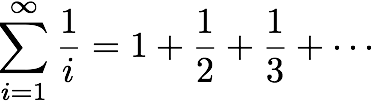
is divergent---the sum does not approach a finite limit..
(a) Evaluate the sum of the first one million terms of this series. To do this, you will need to use the various techniques available in MATLAB for manipulating vectors:
- First create the vector (1,2,....,10000000) and assign it to a variable.
- Then create the vector of reciprocals (1,1/2,1/3,...,1/1000000)
by using componentwise division.
- If v is a vector, then sum(v) is the sum of all the components of
v. (This is not true if v is a matrix with more than one row and more
than one column.)
(b) Now evaluate the sum again, but this time evaluate it as
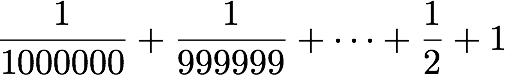
(You can begin by creating a vector
whose components are (1000000,999999,...,1).)
(c)The answers are close, but not exactly equal. Again, you will need to use format long to see this. Which one do you think is more accurate? We will return to this question next week, when we discuss the floating-point representation of numbers in the computer.
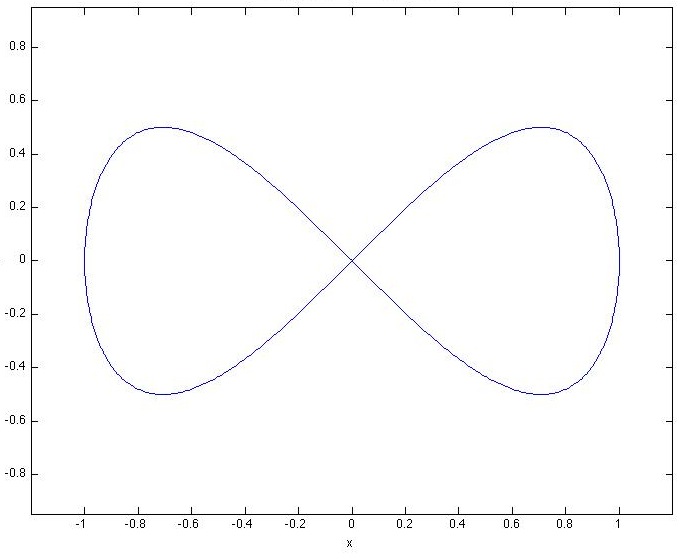
2. Plot the lemniscate of Gerono, pictured above. Parametric equations for the curve are given by
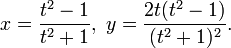
If you try to plot this in the most straightforward way, you are likely to encounter a difficulty connected with the limits on the parameter t, and not be able to produce a smooth plot like the one above. How can you fix this?
3. Plot a "conical helix"
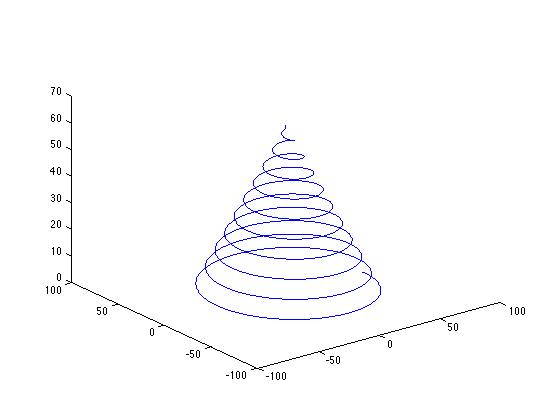
4. Plot a conical surface.
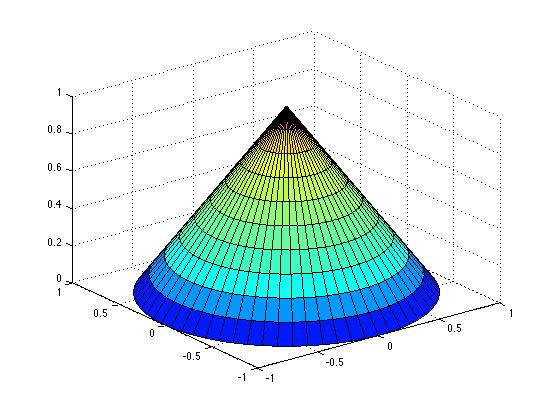
You need a parametrization in terms of two parameters, which you should choose as the distance r from the z-axis and the polar angle u, as above.
What to Hand In:
With this assignment and with all subsequent assignments, you will submit two different things:- A paper document, handed in at the start of class on the due date.
- A zipped folder, submitted through the Blackboard Vista site for this course, before the start of class on the due date.
The folder should contain (a) an electronic copy of the word-processed document you submit in class; (b) the M-files containing the sequences of statements that generate the plots in problems 3-5 --I will execute each of these files to see the result. (c) .jpg files containing the plots (to create these, select Save As.. from the File menu of the window containing the plot, and then select 'JPEG image' for the file format. Place all electronic documents in a folder, compress the folder, submit the resulting .zip file to the Blackboard Vista site for this course. Your name and the assignment number should be part of the name of the folder and in the subject line of the e-mail message.